Abstract

The Reduced Eye Model, introduced more than 150 years ago, uses the refraction of light at a spherical air-water interface to provide a remarkably accurate description of the optics of the human eye. It does not, however, account for the presence of the crystalline eye lens and cannot describe accommodation realistically. The Restored Eye Model, introduced here, is an extension of the Reduced Eye Model by adding a thin lens at the center of curvature of the cornea modeling the crystalline lens. The new model allows for the construction of ray diagrams taking into account both the refraction at the cornea and at the thin lens in the center. It also provides an equation of the image formation in terms of the radius of curvature of the cornea and that of the thin lens using realistic values of the refraction indices of the fluids inside the eye and that of the crystalline lens. This equation makes it possible to describe accommodation realistically as a change in the average curvature of the crystalline eye lens. The Reduced Eye Model is a model of the optics of the eye after an old-fashioned cataract operation where the crystalline lens is taken out but not replaced by an implant. The Restored Eye Model is a model for the optics of the eye after a modern cataract operation where the crystalline eye lens is taken out and replaced by an implant lens. It is also an approximate description of the optics of the human eye.

Keywords: Eye Model, Cornea, Refraction Rays.

Introduction:

Introduction

 Light entering the eye is refracted at the cornea, essentially a spherical surface with a radius of about 5 millimeters. Light rays are transmitted through a few millimeters of aqueous fluid and enter the crystalline eye lens; about 4 millimeters thick, where the rays undergo further refraction. Rays emerging from this lens continue through another aqueous layer of about 15 millimeters to the retina where, ideally, a sharp image is   formed. Figure-1 illustrates the shape of the eye and provides relevant data for the refractive indices. The front surface is the cornea, the object labeled “7/5” represents the crystalline eye lens, the back surface is the retina. The center of curvature of the cornea is very close to the center of the lens. The refractive index outside is equal to 1, that of the fluid between the cornea and the lens is taken as 4/3, very close to the 1.336 [1]. The average

value of the refractive index of the lens is about 7/5. In reality, the lens has a refractive index gradient from 1.415 at the center to 1.37 at the surface [2]. The refractive index of the fluid between the lens and the retina is taken as 4/3, very close to the 1.337 [1].

Figure-1: Approximate Eye Data adapted [1]. The distance from front, cornea, to back, retina, is about 24 millimeters The center of curvature of the cornea is very close to the center of the lens with a radius of about 5 millimeters. The refractive index of the fluid between the cornea and the crystalline eye lens is about 4/3, that of the crystalline eye lens varies between 1.37 and 1.415, with an average value close to 7/5, that of the fluid between the lens and the retina is about 4/3.

 Details of the Reduced Eye Model are described in the book by professor Donders [3]. A schematic diagram of this model is given in Figure 2.

Figure-2: The Reduced Eye Model consists of two interconnected and overlapping spheres filled with water. The smaller sphere representing the curvature of the cornea having radius R, about 5 millimeters, has its center at the nodal point N. This sphere is almost but not completely enclosed by the larger sphere representing the eye ball with diameter D, about 20 millimeters. The distance p represents the amount of protrusion of the cornea from the front of the larger sphere, that is, the distance between the front point of the cornea and the front of the larger sphere along the pupil-fovea-axis. The refractive index outside is equal to 1, and that of the eye interior is 4/3. The crystalline eye lens is absent.

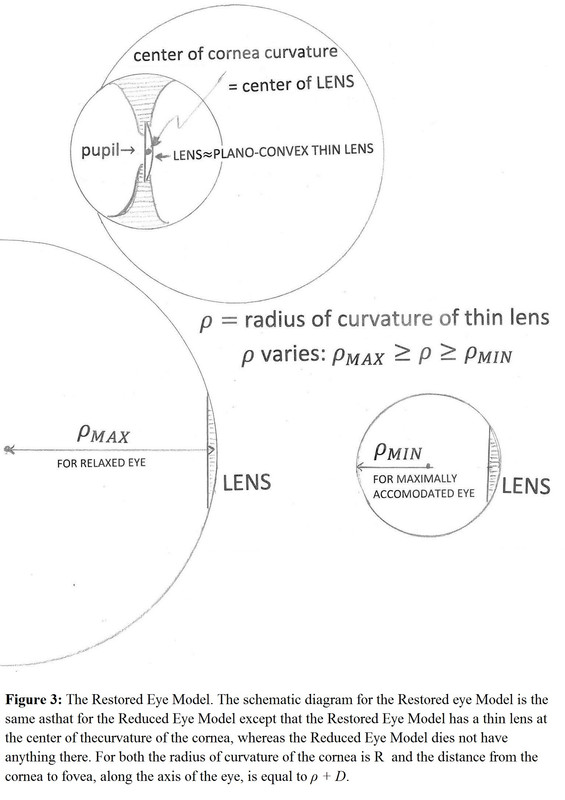
Figure-3: It shows the Restored Eye Model, which is the same as that of the Reduced Eye Model except that it has a thin lens located at the center of cornea curvature. This lens is flat at the front and curved on the back with radius ρ. This radius can vary as a result of accommodation. The index of refraction of this lens is taken as 7/5. The real crystalline lens is not a thick lens with some curvature at the front and more curvature at the back (see figure 1) with a refractive index exhibiting a gradient with higher values at the center and smaller values at the surface [2].

The Reduced Eye Model

Special rays for construction are shown in Appendix A and the equation for the image formation is derived there too. This equation is

where do is the object distance, the distance from an object outside the eye to the cornea, di is the image distance, the distance from the cornea to the image formed by the curved air-water boundary (the cornea) inside the water in the overlapping spheres, and R is the radius of curvature of the cornea as shown in Figure 2. The anterior focal point, FA , correspond with 1 di = 0 , so that this point is in front of  the cornea at a distance of 3R , and the posterior focal point, FP , corresponds with   1 do = 0 , so that that point is behind  the cornea at a distance of 4R from the cornea [3]. The condition of having the image on the retina is:

In this model, emmetropia corresponds to p + d = 4R , myopia to p + D > 4R , hypermetropia to p + D < 4R. The Far-point is given by

Note that this is negative for hypermetropia, meaning that the point is behind the retina. A corrective positive lens can be placed in front of the hypermetropic eye with its focal point at the Far-point.

A corrective negative lens can be placed in front of the myopic eye, also, with its focal point at the corresponding Far-point. The Reduced Eye Model has no realistic mechanism to accommodate. However, for the purpose of teaching the optics of the eye, one can imagine a science-fiction-like “pop-eye” mechanism in which the p can change. For example, with an eye having D = 22 mm, R = 6 mm    , p = 2mm in the relaxed state, but p = 4 mm for the maximally accommodated state, the relaxed eye would have do = ∞ (focusing on the horizon), and the maximally accommodated eye would have  d0 = 234mm (focusing on an object about 23 cm in front of the eye).

The Restored Eye Model

Special rays for construction are shown in Appendix B and the equation for the image formation is derived there too. This equation is:

Discussion

The main difference between an actual healthy eye and the Restored Eye Model is that the eye has a thick lens with a refractive index gradient, whereas the model has a thin lens with a refractive index of 7/5. The error resulting from treating the crystalline eye lens as a thin lens with an average refractive index is not expected to be large. The Restored Eye Model is an accurate description of an eye with an implant lens after cataract surgery. The assumption that the lens is plano-convex instead of having two convex surfaces is irrelevant. Replacing the plano-convex lens with a lens having radii of curvature ρ 1 and ρ2 corresponds with replacing 1/ρ in equation 4 by 1/2 (1/ρ 1 +1/ρ 2).

Acknowledgments

I wish to thank my friend, colleague and former student, Dr. Robert Duvall, O.D., who taught me the anatomy, physiology and optometry of the human eye during the 5 times we co-taught PHYS-359 (Clinical Optics) at WKU, and our current students in this class for their attention, patience and dedication to their Trevor Hoffman, Kelly Nash, Kennedy Neukam, Claire Ottman, Ashley Peterson, Nikil Ravishankar, Dylan  Sanford, Alex Schneller, Chris Sherman, Ethan Smith, Lexie Turpin, Ben Willis and Katie Wilmes. Studies and career goals: Abigail Carver, Sam Ford,

Conflicts of Interest: None

       References

1.      Charman WN, Adnan, Atchison DA. Gradients of refractive index in the crystalline lens and transient changes in refraction among patients with diabetes. Biomed Opt Express. 2012;3(12):3033-42.

2.      F.C. Donders. Accommodation and Refraction of the Eye. Robert E. Krieger Publishing Company. 1979. reprint of the 1864 edition with new introduction.

3.      http://hyperphysics.phy-astr.gsu.edu/hbase/vision/eyescal2.html